Page 78 - 第九版生物化学

厂

第三章酶与酶促反应 63

芘..,,201, 癹..,, 201 ,

HOB: .. /
、 BH 0
H+ 入。H
" " ' )R 2 - N - C - R 1 ? 0 R, 钾:i,
I II
H0 + O=C-R1

—R2 NH2

图 3-10 胰凝乳蛋白酶的催化机制

第三节 酶促反应动力学

酶促反应动力学 (kinetics of enzyme-catalyzed reactions) 是研究酶促反应速率以及各种因素对酶促

反应速率影响机制的科学 。 酶促反应速率可受多种因素的影响，如酶浓度、底物浓度 、 pH 、 温度、抑制

剂及激活剂等 。 研究酶促反应动力学具有重要的理论和实践意义 。

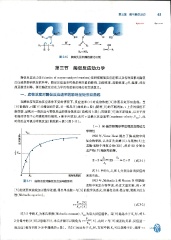
一、底物浓度对酶促反应速率的影响呈矩形双曲线

在酶浓度和其他反应条件不变的情况下，反应速率 (V) 对底物浓度[ s] 作图呈矩形双曲线 。 当

[ s] 很低时， v 随 [SJ 的增加而升高，呈一级反应（曲线的 a 段）；随着[ s] 的不断增加， v 上升的幅度不

断变缓，呈现出一级反应与零级反应的混合级反应（曲线的 b 段）；再随着[ s] 的不断增加，以至千所

有酶的活性中心均被底物所饱和， v 便不再增加，此时 v 达最大反应速率 (maximum velocity, V'""") , 此
时的反应可视为零级反应（曲线的 c 段）（图 3-11) 。

（一）米曼方程揭示单底物反应的动力

V} 学特性
恲 i} 1902 年， Victor Henri 提出了酶－底物中间

A 复合物学说，认为首先是酶 (E) 与底物 (s) 生
成酶－底物中间复合物 (ES), 然后 ES 分解生
龄
话
赵

T1 V-,一一一一一一 成产物 (P) 和游离的酶。

k1 k3 (式 3-1)
E + S~ES------? E +P

k2

式 3-1 中的 kl 、 k2 和 k3 分别为各向反应的

0 K., 底物浓度[SJ 速率常数 。

图 3-11 底物浓度对酶促反应速率的影响 1913 年， Michaelis L 和 Menten M 根据酶－
底物中间复合物学说，经过大量实验，将 v 对

[ s] 的矩形双曲线加以数学处理，得出单底物 v 与[ s] 的数学关系式，即著名的米－曼方程，简称米氏方

程 (Michaelis equation) 。

Vm.. [S] （式 3-2)

v= 凡 +[SJ

式 3-2 中的凡为米氏常数 (M呻aelis constant) , Vmax 为最大反应速率。当 [SJ 远远小于凡时，式 3- ~OTT. t a

2 分母中的[ s] 可以忽略不计，米氏方程可以简化为 v= 二V竺[ SJ, 此时 v 与[ s] 成正比关系，反应呈一

级反应（相当于图 3-10 中曲线的 a 段） 。 当[ s] 远远大于Km凡时，方程中的凡可以忽略不计，此时 V=